Vejam que quanto mais próximo do equador maior o vetor vermelho que representa a força inercial, aquela que tenta arrancar um pedaço do planeta. Isso ocorre porque quanto mais próximo do equador maior é a velocidade linear deste ponto, maior é a circunferência percorrida pelo ponto no mesmo espaço de tempo (uma rotação do planeta). Um ponto situado num dos pólos não sente esta força inercial pois ele não sai do lugar, apenas gira sob o eixo do planeta, já um ponto no equador dá uma volta a cada 10:14 horas e isso representa uma velocidade linear de 37 mil km/h! Um gigantesco carrossel.

Das afirmações acima tiramos uma interessante conclusão: se fosse possível nos colocarmos em pé numa superfície hipotética do planeta Saturno, aquilo que chamamos de vertical não será uma linha que aponte para o centro do planeta. Será, sim, uma linha perpendicular à superfície do planeta no ponto onde estamos "em pé" mas como o planeta não é uma esfera, é achatado, esta linha "vertical" aponta um pouco para fora do centro do planeta. Isso ocorre porque existem duas forças atuando no nosso corpo: a gravidade que puxa aproximadamente para o centro do planeta (depois explico porque é "aproximadamente") e esta força que acabamos de explicar, a inércia da rotação. No desenho acima temos os vetores vermelhos como a força causada pela inércia querendo nos "expulsar" da superfície do planeta numa direção perpendicular ao eixo do mesmo. Esta força resultante da inércia é variável indo do seu máximo no equador até zero nos pólos. No equador ela tende a diminuir o nosso peso pois está exatamente oposta à força da gravidade, nos pólos ela é nula e temos nosso peso máximo mas entre os pólos e o equador a força da inércia forma um ângulo variável com a força da gravidade e por isso a resultante (soma vetorial) varia e causa esta forma achatada no planeta. Vejam que todos os astros que tem rotação apresentam esta forma em maior ou menor escala, tudo depende da velocidade de rotação e da sua densidade (força gravitacional). A nossa Terra tem um achatamento de 0,3%.

Já respondemos a primeira pergunta. Vamos prosseguir com a explicação do que acontece se tentarmos colocar um satélite numa órbita baixa e inclinada.

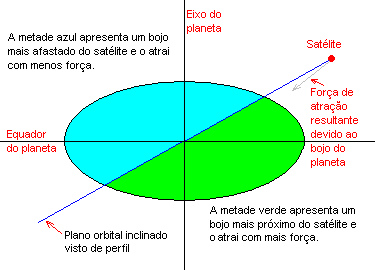
Vejam que o plano orbital (linha azul) do satélite (bolinha vermelha) passa pelo centro do planeta. Isso é óbvio pois quem mantém o satélite em órbita é a atração gravitacional do planeta como um todo e o centro de massa do planeta coincide com seu centro geométrico. Pois bem, para que o satélite se mantenha nesta órbita é necessário que a força atuante nele esteja sempre direcionada para o centro do planeta e no mesmo plano de sua órbita, caso contrário, se existir uma força que atue em outra direção este satélite sairá deste plano orbital e se estabelecerá em outro plano. Agora observe bem que eu dividi o planeta em duas metade de mesma massa usando o próprio plano orbital do satélite. Observe melhor ainda que estas duas metades não estão simetricas em relação ao satélite. Vejam que a metade verde tem um bojo equatorial mais próximo do satélite que o bojo da metade azul que está lá do outro lado. Isso faz com que a força gravitacional resultante seja direcionada um pouco mais na direção do bojo próximo, o verde, e esta força tende a tirar o satélite do seu plano orbital original. Se fizéssemos o desenho para outras órbitas inclinadas ainda teríamos esta força gravitacional levemente para fora do plano. O único lugar onde esta força resultante não apontaria para fora do plano da órbita é quando o plano estiver exatamente no plano equatorial pois aí teremos duas metades exatamente iguais e simétricas. Conclusão: qualquer satélite, ou lua, ou pedregulho, ou grão de poeira que esteja numa órbita inclinada próxima de Saturno tenderá a ir para o plano equatorial do planeta. E é isso que acontece com os seus anéis, eles estão espremidos no plano equatorial devido ao formato achatado do planeta. O mesmo acontece com a as luas próximas de Saturno, estão todas orbitando praticamente no plano equatorial. Na verdade existe outro plano orbital onde poderia haver um equilíbrio instável, são as órbitas polares. Se desenhássemos uma órbita polar ela dividiria o planeta em duas metades simétricas também porém qualquer pequeno desequilíbrio nesta órbita e começaríamos a ter a força inclinada atuando e carregando o satélite para o plano equatorial.
E na Terra? O que acontece? Bem, como eu já disse, a Terra tem uma achatamento muito pequeno, cerca de 0,3%, ela é praticamente uma esfera. Com isso, qualquer plano orbital com qualquer inclinação cortará o planeta em duas metades simétricas. Veja o desenho:

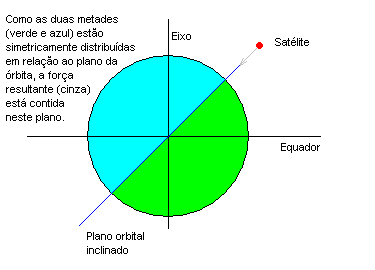
Com isso respondemos a todas as perguntas. Restou explicar por que eu falei lá em cima que a força da gravidade puxa tudo "aproximadamente" para o centro do planeta. Bem, isto já está quase explicado, assim como um satélite numa órbita inclinada "percebe" o planeta como duas metades assimétricas, um corpo na sua superfície também o percebe assim, então, nestes casos de planetas achatados, além daquela força inercial que nos joga para fora do planeta na direção oposta ao eixo do mesmo, aquele bojo que se forma com a rotação também nos puxa um pouco para o lado e não exatamente para o centro do planeta. Como resultado, para que possamos calcular exatamente qual a direção que estamos sendo puxados na superfície do planeta temos que fazer um cálculo interativo onde quanto mais achatamos o planeta, mais distorcemos a direção para a qual a gravidade nos puxa e mais força inercial temos até que atinjamos o ponto de equilíbrio. Isso pode pareceer muito compicado mas basta pensar nas consequências de cada uma destas forças que descrevemos acima para perceber como as coisas funcionam.